Figuras congruentes y semejantes

Las figuras congruentes y semejantes son dos conceptos importantes en la geometría, pero estos  se emplean de distintas maneras  y cumplen con algunos criterios para construir e identificar. A continuación, te mostrarè sus diferencias.

Ejemplos de figuras semejantes

Triángulos Semejantes:

• Triángulos Escalenos: Consideremos un triángulo con lados de longitudes 3 cm, 4 cm y 5 cm. Si multiplicamos todas las longitudes por 2, obtenemos un triángulo con lados de 6 cm, 8 cm y 10 cm. Ambos triángulos son semejantes con una razón de semejanza de 2.
• Triángulos Isósceles: Dos triángulos isósceles con ángulos base iguales son semejantes. Por ejemplo, si tenemos un triángulo isósceles con ángulos de 45 grados en la base, otro triángulo con la misma configuración angular será semejante.

Círculos Semejantes:

• Círculos Concéntricos: Si consideramos dos círculos con el mismo centro y radios diferentes, son círculos semejantes. La razón de semejanza es la razón de los radios.

Cuadrados y Rectángulos:

• Cuadrados Semejantes: Dos cuadrados con lados de longitudes proporcionales son semejantes. Por ejemplo, un cuadrado con lados de 2 cm y otro con lados de 4 cm son semejantes con una razón de semejanza de 2.
• Rectángulos Semejantes: Dos rectángulos con longitudes de lados proporcionales también son semejantes. Si un rectángulo tiene lados de 3 cm y 6 cm, y otro tiene lados de 6 cm y 12 cm, son semejantes con una razón de semejanza de 2.

Polígonos Semejantes:

• Triángulos en General: Dos triángulos cualesquiera con ángulos iguales serán semejantes. Esto se aplica no solo a triángulos específicos, sino a cualquier par de triángulos con ángulos correspondientes iguales.
• Pentágonos y Hexágonos: La semejanza también se puede aplicar a polígonos regulares. Si consideramos dos pentágonos regulares con lados proporcionales, son semejantes.

Estos ejemplos ilustran cómo las figuras semejantes pueden encontrarse en diversas formas geométricas y cómo la razón de semejanza es crucial para establecer la relación entre ellas. La semejanza geométrica proporciona una herramienta valiosa para entender las proporciones y escalas en una variedad de contextos matemáticos y prácticos.

¿Qué son las figuras congruentes?

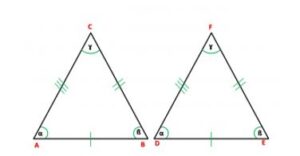Las figuras congruentes son aquellas que son idénticas en forma y tamaño. En el contexto de la geometría, dos figuras son congruentes si tienen la misma medida en todos sus lados y la misma medida en todos sus ángulos correspondientes. La congruencia implica que, al superponer una figura sobre la otra, todas las partes coinciden perfectamente. En resumen, las figuras congruentes son geométricamente idénticas.

Características de las figuras congruentes

Las figuras congruentes comparten varias características distintivas que las definen como idénticas en forma y tamaño. Aquí se presentan las principales características de las figuras congruentes:

Longitudes Iguales:

• Todos los lados correspondientes de figuras congruentes tienen la misma longitud. Si un lado de una figura es "a", el lado correspondiente en la figura congruente también será "a".

Ángulos Iguales:

• Todos los ángulos correspondientes en figuras congruentes son iguales. Esto incluye tanto ángulos internos como externos. Si un ángulo de una figura es de 30 grados, el ángulo correspondiente en la figura congruente será también de 30 grados.

Superposición Exacta:

• Al superponer una figura sobre la otra, todas las partes deben coincidir perfectamente. Esto implica una correspondencia precisa en términos de posición y orientación de las figuras.

Forma Geométrica Idéntica:

• Las figuras congruentes tienen la misma forma geométrica. Esto significa que los ángulos y los lados están dispuestos de la misma manera en ambas figuras.

Tamaño Idéntico:

• No solo comparten forma, sino que también tienen el mismo tamaño. Todas las dimensiones, incluyendo longitudes y ángulos, son iguales entre las figuras congruentes.

Reflexión, Rotación o Traslación:

• Las figuras pueden ser congruentes mediante reflexiones (simetría), rotaciones o traslaciones (movimientos rectilíneos). Estos procesos mantienen la congruencia entre las figuras.

Identidad Geométrica:

• Las figuras congruentes representan una identidad geométrica completa. Todas las características geométricas de una figura son exactamente iguales a las de la figura congruente.

Congruencia en Polígonos y Circunferencias:

• La congruencia se aplica a polígonos, como triángulos, cuadrados y hexágonos, así como a círculos. Dos círculos son congruentes si tienen el mismo radio.

Aplicación en Geometría Euclidiana:

• En geometría euclidiana, la congruencia es una relación fundamental utilizada para establecer la igualdad entre figuras y resolver problemas geométricos.

Utilidad en Demostraciones Geométricas:

• La congruencia se utiliza en demostraciones geométricas para establecer la igualdad entre dos o más figuras, lo que facilita la resolución de problemas y la comprensión de propiedades geométricas.

Estas características destacan la naturaleza precisa y rigurosa de la congruencia geométrica, un concepto central en geometría con amplias aplicaciones tanto teóricas como prácticas.

Ejemplos de figuras congruentes

Triángulos Congruentes:

• Triángulos Equiláteros: Dos triángulos equiláteros con todos los lados de igual longitud son congruentes entre sí.
• Triángulos Isósceles: Dos triángulos isósceles con ángulos y lados congruentes son congruentes.

Cuadrados y Rectángulos:

• Cuadrados Congruentes: Dos cuadrados con lados de igual longitud son congruentes.
• Rectángulos Congruentes: Dos rectángulos con lados y ángulos congruentes son congruentes.

Círculos Congruentes:

• Círculos Idénticos: Dos círculos con el mismo radio son congruentes.

Polígonos Regulares:

• Hexágonos Congruentes: Dos hexágonos regulares con todos los lados y ángulos congruentes son congruentes.

Segmentos de Recta:

• Segmentos de Recta Congruentes: Dos segmentos de recta con la misma longitud son congruentes.

Triángulos Rectángulos Especiales:

• Triángulos 3-4-5: Triángulos rectángulos con lados proporcionales (como 3-4-5) son congruentes entre sí.

Paralelogramos:

• Paralelogramos Congruentes: Dos paralelogramos con lados y ángulos congruentes son congruentes entre sí.

Triángulos Isósceles con Ángulos Correspondientes:

• Triángulos Isósceles Congruentes: Dos triángulos isósceles con ángulos en la base y lados congruentes son congruentes.

Trapecios Isósceles:

• Trapecios Congruentes: Dos trapecios isósceles con ángulos y lados congruentes son congruentes.

Figuras Reflejadas o Rotadas:

• Figuras Reflejadas: Una figura y su imagen reflejada respecto a una línea son congruentes.

Estos ejemplos ilustran la variedad de figuras geométricas que pueden ser congruentes entre sí. En cada caso, las figuras comparten idénticas longitudes y ángulos correspondientes, cumpliendo con la definición de congruencia en geometría.

Criterios de congruencias de los triángulos

1.Lado-Lado-Lado (L, L.L): si los tres lados miden los mismo a lo del otro triangulo, entonces son congruentes.

2.Lado-Ángulos-Lado (L, A,L): Cuando dos triángulos miden iguales en sus ambos lados y si el ángulo tienen la misma apertura, entonces son congruentes.

3.Angulo-Lado-Angulo (A.L.A): Si dos triángulos tienen las mismas medidas en uno de sus lados y los ángulos de su extremos son iguales, entonces son congruentes.

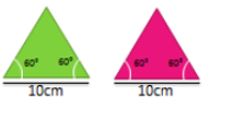
¡ Vamos a practicar!